Bracketing Method#
강좌: 수치해석
그래프를 이용한 방정식 해 찾기#
낙하산병 문제 에서 아래를 상황을 생각해보자.
질량 \(m=68.1kg\)인 낙하산병이 자유낙하할 때 10초 후 속도가 \(40m/s\) 가 되는 항력 계수는 얼마인가?
엄밀해를 이용하면 다음과 같다.
\[
f(c)= \frac{mg}{c} (1 - e^{(-c/m)t}) - 40 = \frac{9.81(68.1)}{c} (1 - e^{(-c/68.1)10})
\]
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150
# 주요 상수
m = 68.1
g = 9.81
t = 10
def f(c):
# using the exact solution
return m*g/c*(1 - np.exp(-c/m*t)) - 40
# 4~20 사이에서 값 계산
for c in range(4, 21, 4):
print(c, f(c))
4 34.19047156669296
8 17.712257537470236
12 6.113943075921462
16 -2.230260706051183
20 -8.368384465361824
# 초기 Guess (0, 20)
c = np.linspace(1, 20, 101)
# Plot
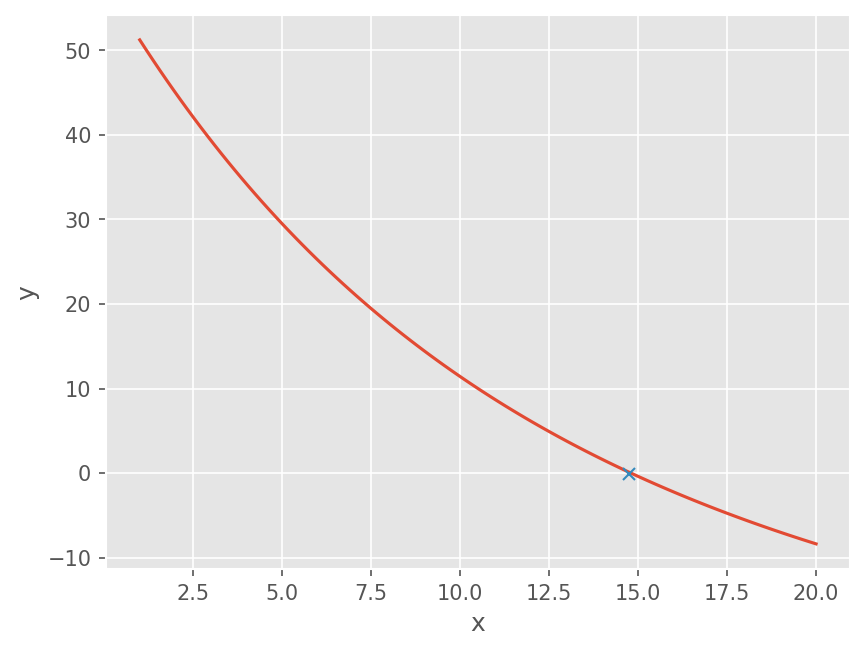
plt.plot(c, f(c))
# From graph
plt.plot(14.75, f(14.75), marker='x')
plt.xlabel('x')
plt.ylabel('y')
Text(0, 0.5, 'y')
Bisection Method#
그래프로 구하는 과정을 체계적으로 생각해보면, 구간을 정하고 양 끝 점에서 부호가 같은지 다른지 확인하고 구간을 줄여 나간다.
\[
f(a)\times f(b) < 0
\]
알고리즘#
해가 구간 (a, b) 사이에 있을 때 해가 존재하면 \(f(a)\cdot f(b) < 0\) 조건을 활용한다.
이 경우 중간 값 \(c=\frac{a+b}{2}\) 에 대해
\(f(a)\cdot f(c) < 0\) 이면 해가 (a, c) 사이에 있다고 범위를 좁힘
\(f(c)\cdot f(b) < 0\) 이면 해가 (c, b) 사이에 있다고 범위를 좁힘
Fig. 6 Bisection method (From Wikipedia)#
By hand#
첫번째 구간을 [12, 16] 으로 한 후 진행해보자
a, b = 12, 16
# Check if the solution lies within the interval [a, b]
f(a)*f(b) < 0
True
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(False, True)
# 범위를 좁힘
a = c
print("New interval: {}".format((a, b)))
New interval: (14.0, 16)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(True, False)
# 범위를 좁힘
b = c
print("New interval: {}".format((a, b)))
New interval: (14.0, 15.0)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(False, True)
# 범위를 좁힘
a = c
print("New interval: {}".format((a, b)))
New interval: (14.5, 15.0)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(False, True)
# 범위를 좁힘
a = c
print("New interval: {}".format((a, b)))
New interval: (14.75, 15.0)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(True, False)
# 범위를 좁힘
b = c
print("New interval: {}".format((a, b)))
New interval: (14.75, 14.875)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(True, False)
# 범위를 좁힘
b = c
print("New interval: {}".format((a, b)))
New interval: (14.75, 14.8125)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(False, True)
# 범위를 좁힘
a = c
print("New interval: {}".format((a, b)))
New interval: (14.78125, 14.8125)
# Midpoint
c = 0.5*(a + b)
# 해가 [a, c]. [c, b] 중 어디에 존재하는지 확인
f(a)*f(c) < 0, f(c)*f(b) < 0
(False, True)
종료 판정 기준#
위 과정은 무한히 계속될 수 있다. 적당한 해상도 이내에서 계산이 되었으면 멈춰야 한다.
즉 오차가 일정 수준 이내, 상대 오차가 일정 수준 이내이면 멈추기로 한다.
엄밀해를 모르므로 근사 상대 오차 \(\epsilon_a\) 의 크기가 \(tol\) 보다 작으면 멈춘다.
Note
\(\epsilon_a< tol\) 이면 멈춘다.
Make a code#
if 구문으로 어떤 쪽으로 선택할 지 만들어 본다.
a, b = 12, 16
c = 0.5*(a+b)
iter_max = 20
for i in range(iter_max):
if f(a)*f(c) < 0:
b = c
elif f(b)*f(c) < 0:
a = c
# Save old midpoint
c0 = c
# Compute new midpoint
c = 0.5*(a + b)
# Compute relative error
if abs((c0 - c)/c) < 1e-6:
# Stop and write converged solution
print("Converged at {}".format(c))
break
else:
print(i, a, b, c)
0 14.0 16 15.0
1 14.0 15.0 14.5
2 14.5 15.0 14.75
3 14.75 15.0 14.875
4 14.75 14.875 14.8125
5 14.75 14.8125 14.78125
6 14.78125 14.8125 14.796875
7 14.796875 14.8125 14.8046875
8 14.796875 14.8046875 14.80078125
9 14.80078125 14.8046875 14.802734375
10 14.80078125 14.802734375 14.8017578125
11 14.80078125 14.8017578125 14.80126953125
12 14.80078125 14.80126953125 14.801025390625
13 14.801025390625 14.80126953125 14.8011474609375
14 14.801025390625 14.8011474609375 14.80108642578125
15 14.80108642578125 14.8011474609375 14.801116943359375
16 14.801116943359375 14.8011474609375 14.801132202148438
Converged at 14.801139831542969
엄밀해가 \(c = 14.8011\) 임을 이용해서 상대오차를 구해보자.
a, b = 12, 16
c = 0.5*(a+b)
c_ex = 14.8011
# 상대오차 (참, 근사)
eps_t = []
eps_a = []
iter_max = 20
for i in range(iter_max):
if f(a)*f(c) < 0:
b = c
elif f(b)*f(c) < 0:
a = c
# Save old midpoint
c0 = c
# Compute new midpoint
c = 0.5*(a + b)
# Compute relative error
eps_ti = abs((c - c_ex)/c)
eps_ai = abs((c0 - c)/c)
eps_t.append(eps_ti)
eps_a.append(eps_ai)
if eps_ai < 1e-6:
# Stop and write converged solution
print("Converged at {}".format(c))
break
else:
print(i, a, b, c, eps_ti, eps_ai)
0 14.0 16 15.0 0.013260000000000004 0.06666666666666667
1 14.0 15.0 14.5 0.020765517241379306 0.034482758620689655
2 14.5 15.0 14.75 0.0034644067796610117 0.01694915254237288
3 14.75 15.0 14.875 0.004968067226890762 0.008403361344537815
4 14.75 14.875 14.8125 0.0007696202531645622 0.004219409282700422
5 14.75 14.8125 14.78125 0.0013429175475687051 0.0021141649048625794
6 14.78125 14.8125 14.796875 0.0002855332629355809 0.0010559662090813093
7 14.796875 14.8125 14.8046875 0.00024232189973615295 0.0005277044854881266
8 14.796875 14.8046875 14.80078125 2.1536025336495212e-05 0.0002639218791237794
9 14.80078125 14.8046875 14.802734375 0.00011041034437261371 0.00013194352816994325
10 14.80078125 14.802734375 14.8017578125 4.444151217259871e-05 6.597611664577422e-05
11 14.80078125 14.8017578125 14.80126953125 1.145383168937938e-05 3.298914657077821e-05
12 14.80078125 14.80126953125 14.801025390625 5.040824742262857e-06 1.6494845360824743e-05
13 14.801025390625 14.80126953125 14.8011474609375 3.2065714921990636e-06 8.247354660992487e-06
14 14.801025390625 14.8011474609375 14.80108642578125 9.171096201613302e-07 4.123694335281092e-06
15 14.80108642578125 14.8011474609375 14.801116943359375 1.1447351872102123e-06 2.0618429164355686e-06
16 14.801116943359375 14.8011474609375 14.801132202148438 2.175654402499187e-06 1.030920395419827e-06
Converged at 14.801139831542969
plt.semilogy(eps_t)
plt.semilogy(eps_a)
plt.legend(['True', 'Approximation'])
plt.xlabel('Iter')
plt.ylabel('Error')
Text(0, 0.5, 'Error')
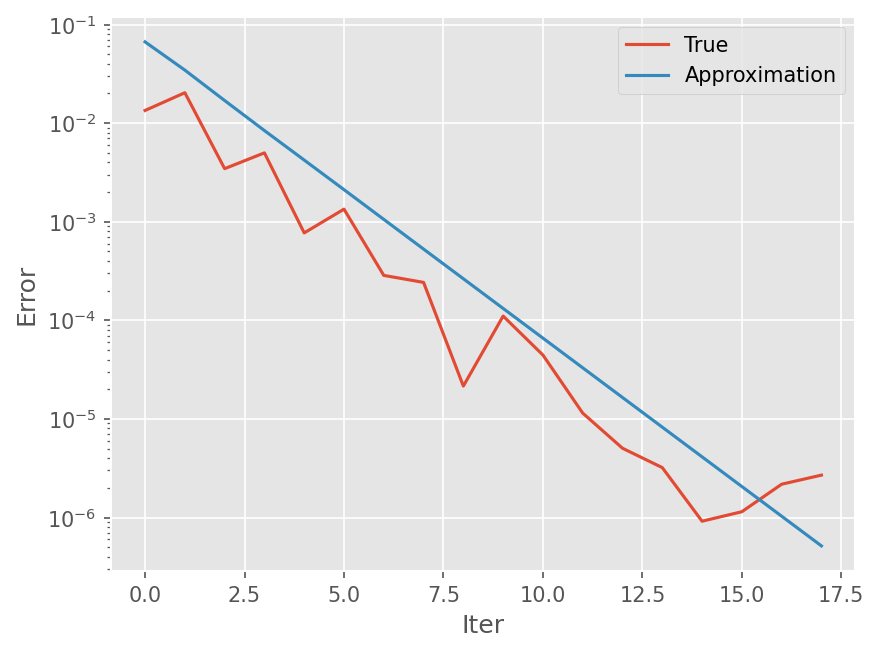
Bisection method를 진행하면서 오차의 범위가 절반씩 줄어든다.
Recursive algorithm#
함수 안에서 함수를 호출
Fig. 7 Recursive algorihm (From Wikipedia)#
Note
\(\epsilon_a\) 계산시 \(c=0\) 일 때 분모가 0이 될 수 있다. 분모에 매우 작은 값을 더하자.
def bisect(a, b, f, c0=a, tol=1e-6):
"""
Bisection method
Parameters
----------
a : float
Lower limit
b : float
Upper limit
c0 : float
Previous solution
f : function
함수
tol : float
Tolerance
"""
fa, fb = f(a), f(b)
product = fa*fb
# 구간 경계에서 해가 존재한 경우
if product == 0:
if fa == 0:
print('Converged at {:.7g}'.format(a))
return a
else:
print('Converged at {:.7g}'.format(b))
return b
elif product > 0:
# 같은 부호 이므로 이 구간 내에 해가 존재하지 않음
raise ValueError('Wrong Intervals')
else:
c = 0.5*(a+b)
# Convergence 조건
if (abs(c - c0)/ max(abs(c), tol)) < tol:
print('Converged at {:.7g}'.format(c))
return c
elif fa*f(c) < 0:
# 해는 (a,c) 사이에 존재함, 범위 좁히기
bisect(a, c, f, c, tol)
else:
# 해는 (c,a) 사이에 존재함, 범위 좁히기
bisect(c, b, f, c, tol)
bisect(12, 16, f)
Converged at 14.80114
구간 설정#
Bracketing method는 적절한 구간 설정이 중요함
1개의 해를 포함하는 구간을 설정해야 함
x = np.arange(-10, 10, 0.1)
def f1(x):
return x**2 + 10*np.sin(x)
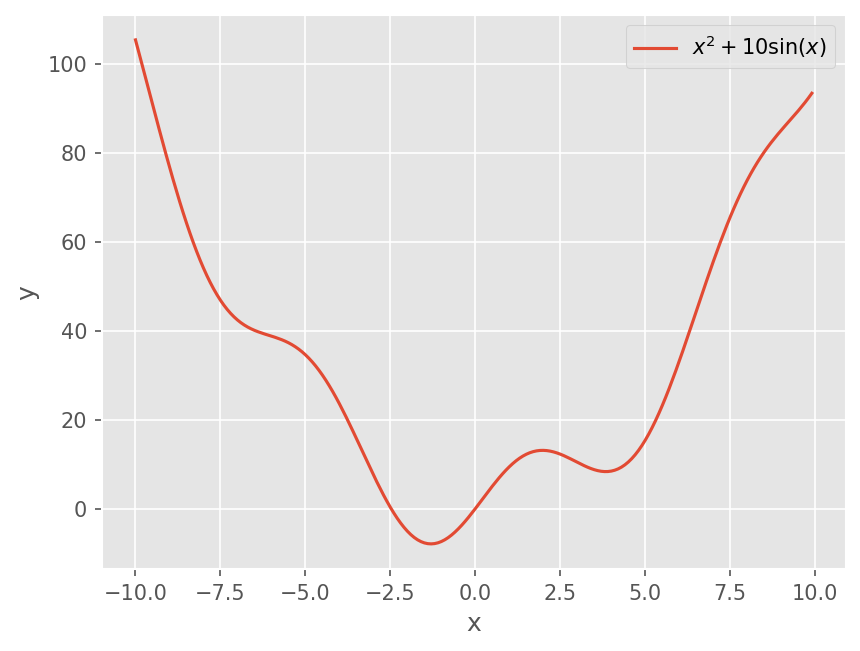
plt.plot(x, f1(x))
plt.xlabel('x')
plt.ylabel('y')
plt.legend(["$x^2 + 10\sin(x)$"])
<matplotlib.legend.Legend at 0x7fde988f8350>
# Left solution
bisect(-10, -1, f1)
Converged at -2.479483
f1(0)
0.0
# Right solution
bisect(-1, 1, f1)
Converged at 0
# Wrong Interval 1
bisect(-10, -5, f1)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In [30], line 2
1 # Wrong Interval 1
----> 2 bisect(-10, -5, f1)
Cell In [24], line 34, in bisect(a, b, f, c0, tol)
30 return b
32 elif product > 0:
33 # 같은 부호 이므로 이 구간 내에 해가 존재하지 않음
---> 34 raise ValueError('Wrong Intervals')
36 else:
37 c = 0.5*(a+b)
ValueError: Wrong Intervals
# Wrong Interval 2
bisect(-5, 5, f1)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In [31], line 2
1 # Wrong Interval 2
----> 2 bisect(-5, 5, f1)
Cell In [24], line 34, in bisect(a, b, f, c0, tol)
30 return b
32 elif product > 0:
33 # 같은 부호 이므로 이 구간 내에 해가 존재하지 않음
---> 34 raise ValueError('Wrong Intervals')
36 else:
37 c = 0.5*(a+b)
ValueError: Wrong Intervals
DIY#
For-Loop 를 이용하여 Bisection method 계산 함수를 만드시오. 아래 기능도 같이 구현하시오.
boolean 형식의 verbose keyword argument를 추가하라.
True 일 경우 중간 계산 결과 및 상대 오차를 출력한다.
False 일 경우 최종 해만 출력한다.
기본 값은 False로 한다.
Method of False Position#
Bisection method 보다 계산 효율을 높이기 위해 가 위치 (False position)를 사용한다.
이 위치는 중점 대신에 양 끝점을 직선으로 이었을 때 교점을 사용한다.
아래 그림을 보면 다음 관계로 가 위치를 구한다.
\[
\frac{f(a)}{c - a} = \frac{f(b)}{c - b}
\]
이를 정리하면 다음과 같다.
\[
c = \frac{b f(a) - a f(b)} {f(a) - f(b)} = b - \frac{f(b)(a-b)}{f(a) - f(b)}
\]
Fig. 8 Method of false position (From Wikimedia)#
알고리즘#
해가 구간 (a, b) 사이에 있을 때 해가 존재하면 \(f(a)\cdot f(b) < 0\) 조건을 활용한다.
이 경우 중간 값 \(c=b - \frac{f(b)(a-b)}{f(a) - f(b)}\) 에 대해
\(f(a)\cdot f(c) < 0\) 이면 해가 (a, c) 사이에 있다고 범위를 좁힘
\(f(c)\cdot f(b) < 0\) 이면 해가 (c, b) 사이에 있다고 범위를 좁힘
a, b = 12, 16
c = b - f(b)*(a-b)/(f(a) - f(b))
c_ex = 14.8011
# 상대오차 (참, 근사)
eps_t = []
eps_a = []
iter_max = 20
for i in range(iter_max):
if f(a)*f(c) < 0:
b = c
elif f(b)*f(c) < 0:
a = c
# Save old midpoint
c0 = c
# Compute new midpoint
c = b - f(b)*(a-b)/(f(a) - f(b))
# Compute relative error
eps_ti = abs((c - c_ex)/c)
eps_ai = abs((c0 - c)/c)
eps_t.append(eps_ti)
eps_a.append(eps_ai)
if eps_ai < 1e-6:
# Stop and write converged solution
print("Converged at {}".format(c))
break
else:
print(i, a, b, c, eps_ti, eps_ai)
0 12 14.930869492487908 14.815076015455954 0.0009433644107781617 0.007815921896799652
1 12 14.815076015455954 14.802632653525668 0.00010353925288440446 0.0008406181671557055
2 12 14.802632653525668 14.80129662906239 1.328458359549417e-05 9.026401515760205e-05
3 12 14.80129662906239 14.801153195602156 3.594017402097734e-06 9.690694930243335e-06
4 12 14.801153195602156 14.801137796968773 2.5536529212191533e-06 1.040368219980068e-06
Converged at 14.801136143814386
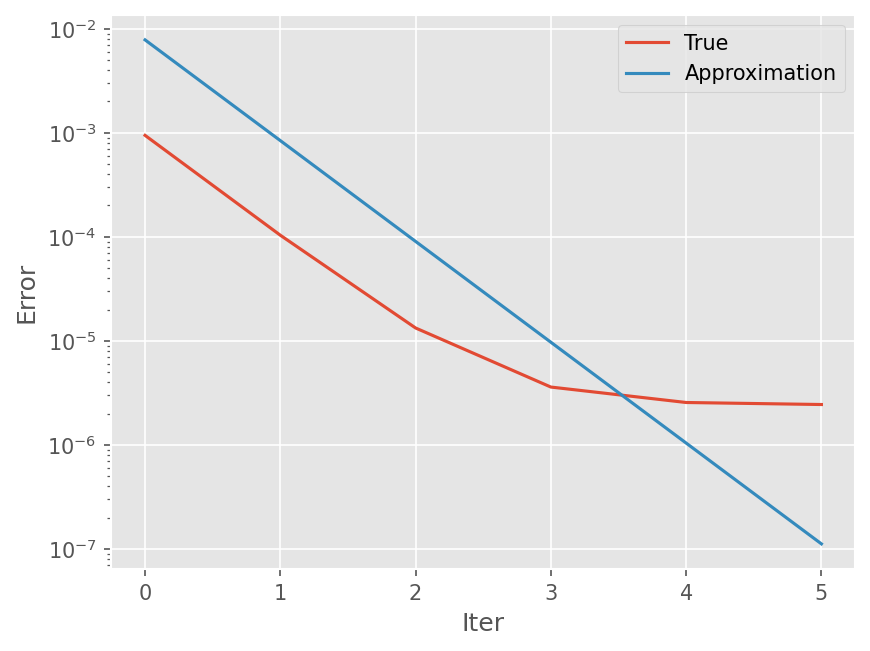
plt.semilogy(eps_t)
plt.semilogy(eps_a)
plt.legend(['True', 'Approximation'])
plt.xlabel('Iter')
plt.ylabel('Error')
Text(0, 0.5, 'Error')
DIY#
Method of False Position 함수를 For-loop 버전과 Recursive algorithm 버전으로 완성하시오.
문제점#
곡률이 큰 함수에서 수렴이 매우 느릴 수 있다.
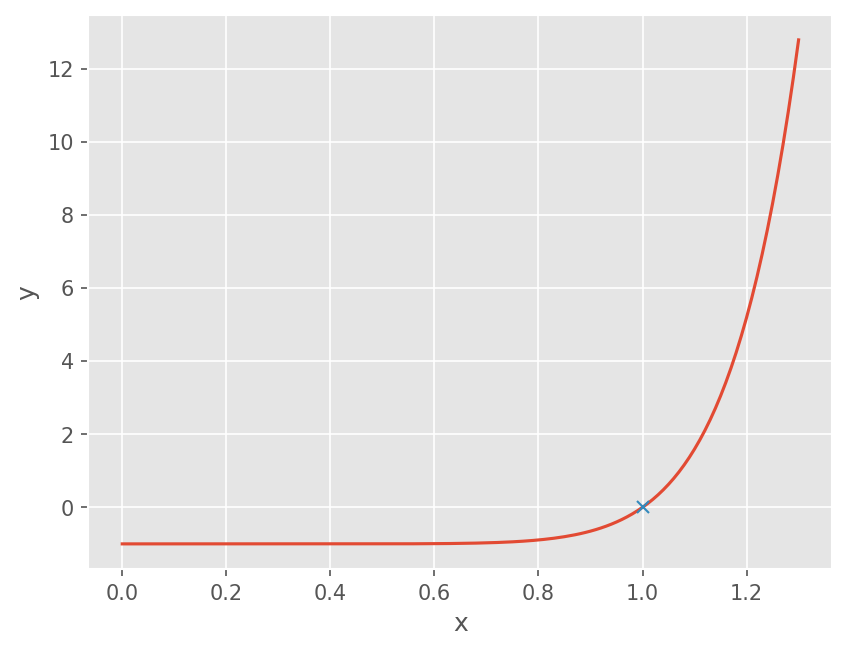
x 가 \([0, 1.3]\) 사이일 때 아래 함수의 해를 구하시오.
\[
f(x) = x^{10} - 1
\]
# 함수 정의
f = lambda x : x**10 - 1
x = np.linspace(0, 1.3, 131)
plt.plot(x, f(x))
plt.plot([1], [0], marker='x')
plt.xlabel('x')
plt.ylabel('y')
Text(0, 0.5, 'y')
a, b = 0, 1.3
c = 0.5*(a+b)
c_ex = 1
# 상대오차 (참, 근사)
eps_t = []
eps_a = []
# 해석 결과
cs = []
iter_max = 25
for i in range(iter_max):
if f(a)*f(c) < 0:
b = c
elif f(b)*f(c) < 0:
a = c
# Save old midpoint
c0 = c
# Compute new midpoint
c = 0.5*(a + b)
cs.append(c)
# Compute relative error
eps_ti = abs((c - c_ex)/c)
eps_ai = abs((c0 - c)/c)
eps_t.append(eps_ti)
eps_a.append(eps_ai)
if eps_ai < 1e-6:
# Stop and write converged solution
print("Converged at {}".format(c))
break
else:
print(i, a, b, c, eps_ti, eps_ai)
0 0.65 1.3 0.9750000000000001 0.025641025641025546 0.33333333333333337
1 0.9750000000000001 1.3 1.1375000000000002 0.12087912087912102 0.1428571428571429
2 0.9750000000000001 1.1375000000000002 1.0562500000000001 0.053254437869822605 0.07692307692307696
3 0.9750000000000001 1.0562500000000001 1.015625 0.015384615384615385 0.04000000000000013
4 0.9750000000000001 1.015625 0.9953125 0.004709576138147522 0.020408163265306076
5 0.9953125 1.015625 1.00546875 0.005439005439005351 0.01010101010100997
6 0.9953125 1.00546875 1.000390625 0.00039047247169083456 0.005076142131979517
7 0.9953125 1.000390625 0.9978515625000001 0.0021530632217654447 0.002544529262086536
8 0.9978515625000001 1.000390625 0.9991210937500001 0.0008796794057275569 0.0012706480304956191
9 0.9991210937500001 1.000390625 0.9997558593750001 0.0002442002442001331 0.0006349206349206127
10 0.9997558593750001 1.000390625 1.0000732421875 7.323682347488755e-05 0.00031735956839092034
11 0.9997558593750001 1.0000732421875 0.9999145507812501 8.545652094281841e-05 0.00015870496746539284
12 0.9999145507812501 1.0000732421875 0.9999938964843751 6.103552878041541e-06 7.934618741565026e-05
13 0.9999938964843751 1.0000732421875 1.0000335693359377 3.356820907519036e-05 3.9671519816012954e-05
14 0.9999938964843751 1.0000335693359377 1.0000137329101564 1.3732721566151756e-05 1.9836153373182286e-05
15 0.9999938964843751 1.0000137329101564 1.0000038146972656 3.8146827137652828e-06 9.918175055922961e-06
16 0.9999938964843751 1.0000038146972656 0.9999988555908204 1.1444104893169604e-06 4.9591121205215245e-06
17 0.9999988555908204 1.0000038146972656 1.0000013351440429 1.3351422602726969e-06 2.4795499119667293e-06
18 0.9999988555908204 1.0000013351440429 1.0000000953674317 9.536742263449668e-08 1.2397764929161892e-06
Converged at 0.999999475479126
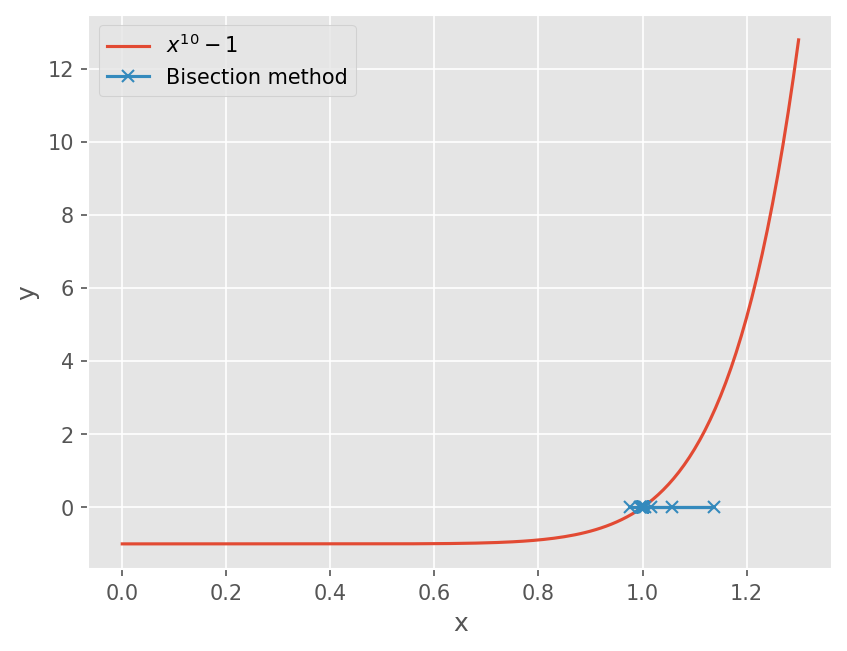
x = np.linspace(0, 1.3, 131)
plt.plot(x, f(x))
plt.plot(cs, np.zeros_like(cs), marker='x')
plt.legend(["$x^{10} -1$", 'Bisection method'])
plt.xlabel('x')
plt.ylabel('y')
Text(0, 0.5, 'y')
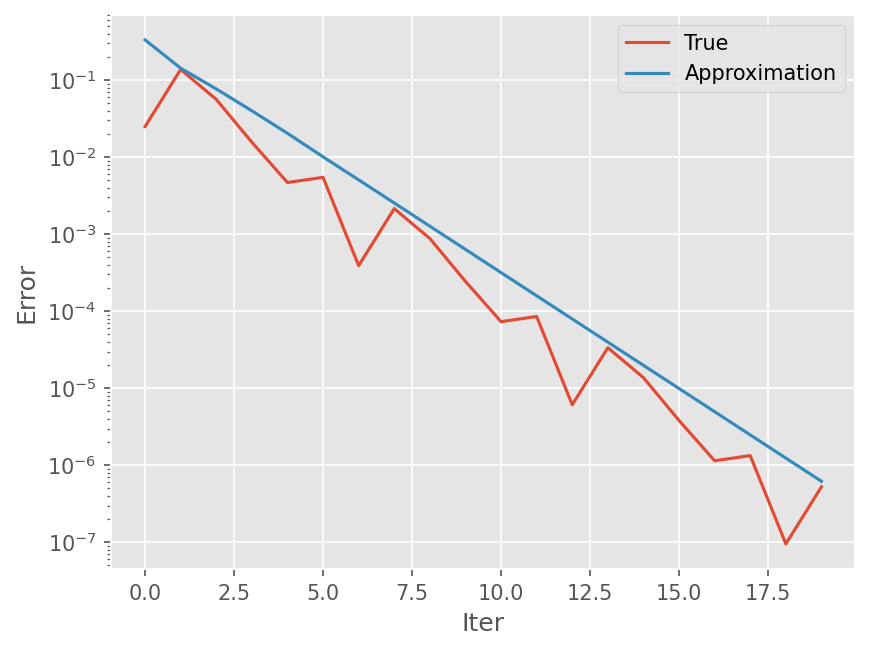
plt.semilogy(eps_t)
plt.semilogy(eps_a)
plt.legend(['True', 'Approximation'])
plt.xlabel('Iter')
plt.ylabel('Error')
Text(0, 0.5, 'Error')
a, b = 0, 1.3
c = b - f(b)*(a-b)/(f(a) - f(b))
c_ex = 1
# 상대오차 (참, 근사)
eps_t = []
eps_a = []
# 해석 결과
cs = []
iter_max = 25
for i in range(iter_max):
if f(a)*f(c) < 0:
b = c
elif f(b)*f(c) < 0:
a = c
# Save old midpoint
c0 = c
# Compute new midpoint
c = b - f(b)*(a-b)/(f(a) - f(b))
cs.append(c)
# Compute relative error
eps_ti = abs((c - c_ex)/c)
eps_ai = abs((c0 - c)/c)
eps_t.append(eps_ti)
eps_a.append(eps_ai)
if eps_ai < 1e-6:
# Stop and write converged solution
print("Converged at {}".format(c))
break
else:
print(i, a, b, c, eps_ti, eps_ai)
0 0.09429959537232735 1.3 0.1817588725190793 4.501794691728348 0.48118298674839827
1 0.1817588725190793 1.3 0.2628740125203042 2.804103686068096 0.3085704030745893
2 0.2628740125203042 1.3 0.3381051033222693 1.9576601777786151 0.22250800139581925
3 0.3381051033222693 1.3 0.4078779165927523 1.4517140039195966 0.17106298338811027
4 0.4078779165927523 1.3 0.4725831535623899 1.116029724000691 0.13691820472626154
5 0.4725831535623899 1.3 0.5325715106320141 0.8776821141132359 0.11263906512467173
6 0.5325715106320141 1.3 0.5881445691706797 0.7002622355419552 0.09448877274685547
7 0.5881445691706797 1.3 0.6395439707682155 0.5636141464969289 0.08036883145938375
8 0.6395439707682155 1.3 0.6869431667412387 0.45572450300926454 0.06900017100086796
9 0.6869431667412387 1.3 0.7304464366929376 0.3690257762464468 0.05955709791488338
10 0.7304464366929376 1.3 0.7700987444968072 0.29853477511304527 0.05148990059681097
11 0.7700987444968072 1.3 0.8059075090169237 0.24083717897086934 0.044432846349573514
12 0.8059075090169237 1.3 0.8378738914244523 0.19349702889049372 0.03815178242776284
13 0.8378738914244523 1.3 0.8660276320873558 0.15469756731633996 0.03250905585430972
14 0.8660276320873558 1.3 0.8904572813509997 0.12301849953183873 0.02743494806014644
15 0.8904572813509997 1.3 0.9113282513082279 0.09729946214712669 0.022901704108555406
16 0.9113282513082279 1.3 0.9288846695992142 0.07655991397884723 0.01890053616512088
17 0.9288846695992142 1.3 0.9434360517492835 0.05995525414344491 0.015423813965015026
18 0.9434360517492835 1.3 0.955333975192147 0.04675435603435884 0.012454203191580743
19 0.955333975192147 1.3 0.9649455723416893 0.03632788072517092 0.009960766104369261
20 0.9649455723416893 1.3 0.9726296888054463 0.028140526152526824 0.007900351544064411
21 0.9726296888054463 1.3 0.9787191336334623 0.02174358877355671 0.00622185121221563
22 0.9787191336334623 1.3 0.9835099523268419 0.01676652852789647 0.004871144091674134
23 0.9835099523268419 1.3 0.9872569173655359 0.012907564799311435 0.0037953292327316803
24 0.9872569173655359 1.3 0.9901736307394302 0.00992388501926856 0.0029456585020510096
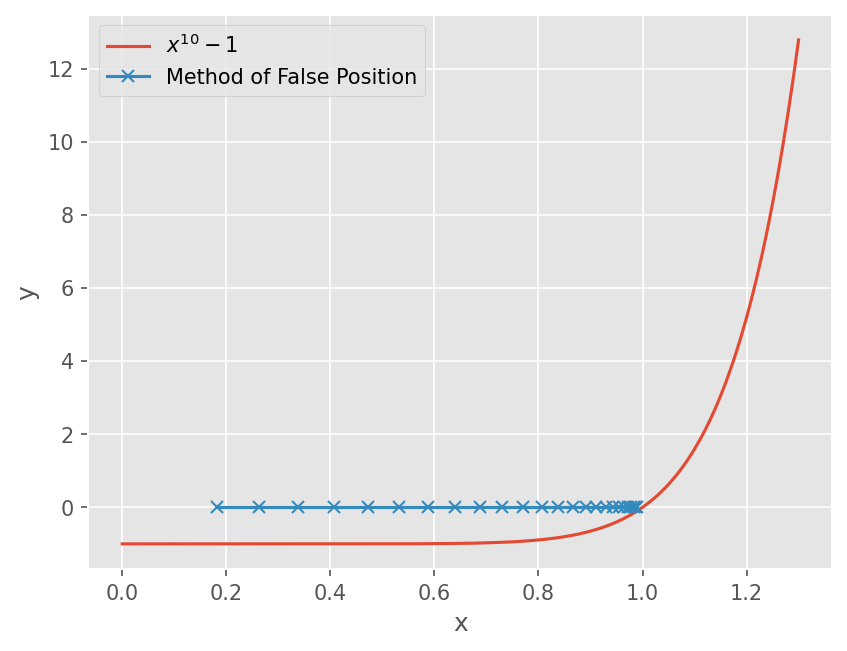
x = np.linspace(0, 1.3, 131)
plt.plot(x, f(x))
plt.plot(cs, np.zeros_like(cs), marker='x')
plt.legend(["$x^{10} -1$", 'Method of False Position'])
plt.xlabel('x')
plt.ylabel('y')
Text(0, 0.5, 'y')
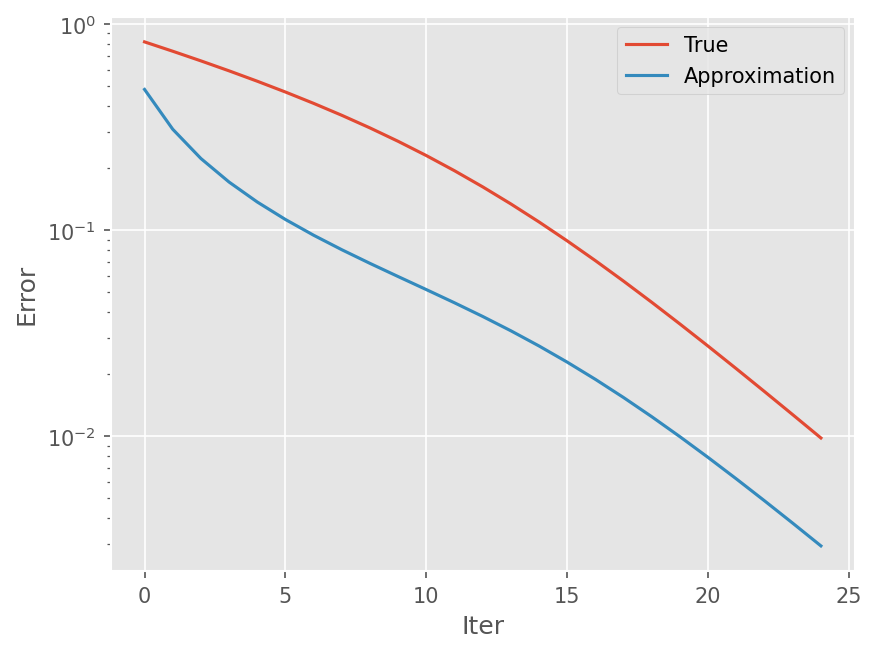
plt.semilogy(eps_t)
plt.semilogy(eps_a)
plt.legend(['True', 'Approximation'])
plt.xlabel('Iter')
plt.ylabel('Error')
Text(0, 0.5, 'Error')
SciPy 활용#
scipy.optimize 모듈은 최소화, Curve fitting 그리고 root finding과 관련된 다양한 알고리듬을 제공한다.
참고
from scipy.optimize import root_scalar
# root_scalar?
root_scalar(f, bracket=[0, 1.3])
converged: True
flag: 'converged'
function_calls: 10
iterations: 9
root: 0.9999999999998475